第七章  第二节  轴向拉伸与压缩

一． 轴向拉伸与压缩的概念

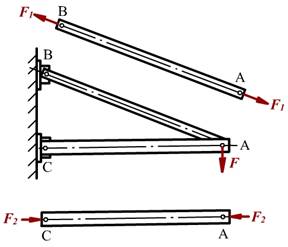
工程实例

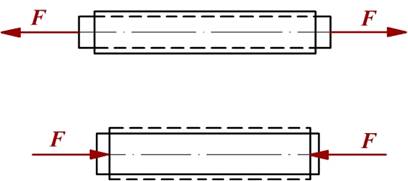
力学模型

受力特点：直杆，所受外力或其合力与杆轴线重合 。

变形特点：沿轴线方向将发生伸长或缩短变形。

杆件的这种变形形式称为杆件的轴向拉伸与压缩。

发生轴向拉伸与压缩的杆件一般简称为拉(压)杆。

二．拉(压)杆的轴力和轴力图

内力的概念

外力——杆件以外物体对杆件的作用力。

     （前面研究的力，主动力和约束反力）

内力——外力引起的物体内部的作用力。 

（物体本来存在内部作用力，外力引起了内部作用力的改变）

也称为附加内力。

    拉(压)杆在外力作用下产生变形，内部材料微粒之间的相对位置发生了改变，其相互作用力也发生了改变。这种由外力引起的杆件内部相互作用力的改变量，称为内力。

内力的特点：1）完全由外力引起，并随着外力改变而改变；

  2）这个力若超过了材料所能承受的极限值，杆件就要断裂；

  3）内力反映了材料对外力有抗力，并传递外力。

    内力的大小和分布形式与杆件的承载能力密切相关。为了保证杆件在外力作用下安全可靠地工作，必须弄清楚杆件的内力。

截面法——用截面假想地把构件分成两部分，以显示并确定内力的方法。

拉(压)杆的内力——轴力以轴向拉伸杆为例，用截面法求得任一横截面m-m上的内力

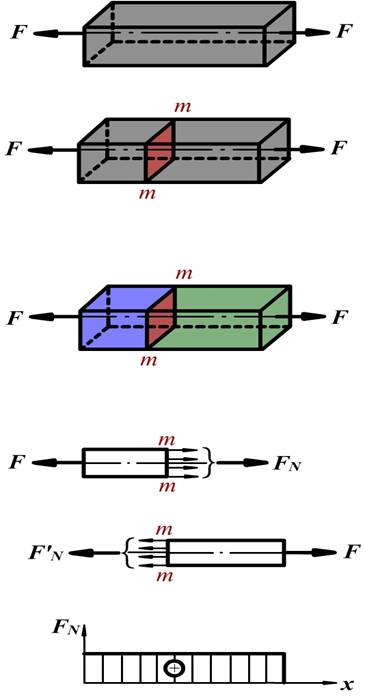
    F'_N与F_N是一对作用力与反作用力。因此，无论研究截面左段求出的内力F_N，还是研究截面右段求出的内力F'_N，都是m－m截面的内力。

    为了使取左段或取右段求得的同一截面上的轴力相一致，规定其正负号为：轴力F_N的符号由变形决定——拉伸时，为正；压缩时，为负。

截面法:

（1）截——沿欲求内力的截面上假想地用一截面把杆件分为两段； 

（2）弃——抛弃一段(左段或右段)，保留另一段为研究对象； 

（3）代——将抛弃段对保留段截面的作用力，用内力F_N代替； 

（4）平——列平衡方程式求出该截面内力的大小。

截面法是求内力最基本的方法。

注意:1）外力不能沿作用线移动——力的可传性不成立；变形体，不是刚体 

     2）截面不能切在外力作用点处——要离开作用点。

轴力图——用平行于杆轴线的x坐标表示横截面位置，用垂直于x的坐标F_N表示横截面轴力的大小，按选定的比例，把轴力表示在x-F_N坐标系中，描出的轴力随截面位置变化的曲线。

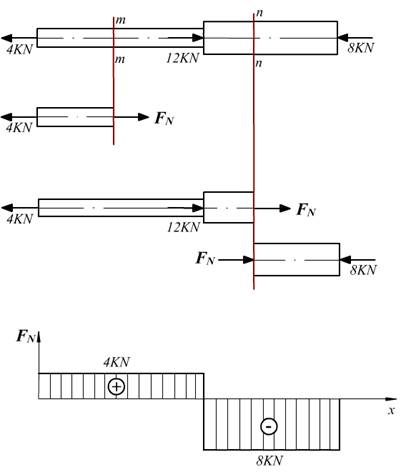
例4-1 图4-2-2a所示的等截面直杆，受轴向力F₁=15KN，F₂=10KN的作用，求出杆件1-1、2-2截面的轴力，并画出轴力图。

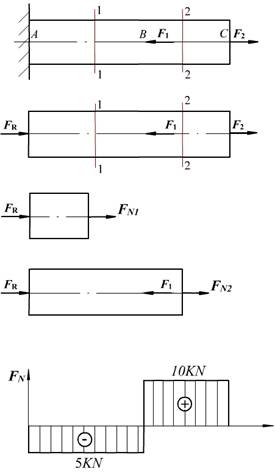
解 (1)外力分析 先解除约束，画杆件的受力图。

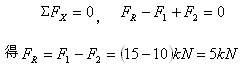
(2)内力分析 外力F_R，F₁，F₂将杆件分为AB段和BC段，在AB段，用1-1截面将杆件截分为两段，取左段为研究对象，

右段对截面的作用力用F_N1来代替。假定内力F_N1为正，列平衡方程

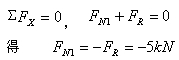
(3)画轴力图

三．横截面的应力

应力的概念

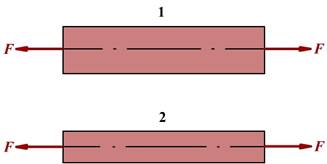
    在相同的F力作用下，杆2首先破坏，而二杆各横截面上的内力是相同的，只是内力在二杆横截面上的聚集程度不一样，这说明杆件的破坏是由内力在截面上的聚集程度决定的。

    内力在截面上分布的密集程度。把内力在截面上的集度称为应力，其中垂直于杆横截面的应力称为正应力，平行于横截面的应力称为切应力。

应力：内力所在截面单位面积上的内力。

在力学中，一般要将p分解：一个分量垂直于截面， 一个分量平行于截面。

——正应力      ——切应力

应力的单位：力的单位/面积的单位    1N/m²=1Pa（帕）

常用1N/mm²=1MPa（兆帕）=10⁶N/m²=10⁶Pa（帕）

  常采用N、mm、MPa的计量单位           

拉(压)杆横截面上的应力

观察杆件变形：外力F使杆件拉伸。可以看到横向线平行向外移动并与轴线保持垂直。

变形现象：各条横向线都作了相对的平移；

任意两条横向线之间的纵向线伸长均相同。

平面假设：    变形前为平面的横截面，变形后仍为平面，仅仅沿轴线方向平移一个段距离。也就是杆件在变形过程中横截面始终为平面。

实质：发生均匀的伸长变形

    根据材料均匀性假设，设想杆件是由无数纵向纤维所组成，任一横截面处轴线方向均匀伸长，横截面上的分布内力（轴力）也应均匀，且方向垂直于横截面。

横截面存在正应力

正应力s的符号规定与F_N一致。 拉应力为“正”；压应力为“负”。式中， F_N表示横截面轴力（N）； A表示横截面面积（mm²）。

四．拉(压)杆的变形

1．绝对变形

轴向变形——拉(压)杆的纵向伸长(或缩短)量，用△L表示；

△L=L₁- L     拉伸时为“正”；压缩时为“负”。

横向变形——横向缩短(或伸长)量，用△d 表示。

△d =d₁- d     拉伸时为“负”；压缩时为“正”。

绝对变形——△L、 △d 。

2．相对变形

    绝对变形与杆件的原长有关，不能准确反映杆件变形的程度，消除杆长的影响，得到单位长度的变形量。

相对变形——单位长度的变形量

 和都是无量纲量，又称为线应变。

—轴向线应变，—横向线应变。

3．横向变形系数

实验表明，当应力不超过某一限度时，其横向线应变与轴向线应变的比值为一常数，记作，称为横向变形系数或泊松比

几种常用工程材料的值见表

虎克定律——对拉(压)杆，当应力不超过某一限度（在弹性范围内）时，杆的轴向变形△L与轴力F_N成正比，与杆长L成正比，与横截面面积A成反比。(反映了力与变形之间的物理关系)

引入比例常数E ，其公式为

       E——材料的拉(压)弹性模量，

    由于轴力、杆长、截面面积相同的等直杆，E值越大，△L就越小，所以E值代表了材料抵抗拉(压)变形的能力，是衡量材料刚度的指标。

量纲为[力]/[长度]²，其单位是GPa，1MPa＝10⁶Pa，1GPa＝10⁹Pa

各种材料的弹性模量E是由实验测定的。几种常用材料的E值见表。

EA——由于拉(压)杆的横截面积A和材料弹性模量E的乘积与杆件的变形成反比，EA值越大，△L就越小，拉(压)杆抵抗变形的能力就越强，所以，EA值表征杆件抵抗轴向拉压变形的能力，称为杆件的抗拉(压)刚度。

公式两边同除以△L，（=F_N／A）

上式表明，当应力不超过某一极限值时，应力与应变成正比。

注意适用条件：应力不超过某一极限值，这一极限值是指材料的比例极限，各种材料的比例极限可由实验测定。在式中长度L内，F_N、E、A均为常量，否则，应分段计算。

例题一构件如图所示，已知：F₁=30kN, F₂=10kN, A_AB=A_BC=500mm², A_CD=200mm², E=200GPa。试求：(1) 各段杆横截面上的内力和应力；(2) 杆的总伸长。

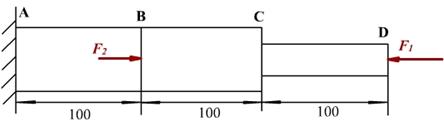
    虽然杆AD不满足虎克定律的适用条件，但AB段、BC段和CD却能分别满足虎克定律，因此，我们可按胡克定律分别求AB、BC、CD三段杆的伸长量，然后相加得到杆AD的总伸长量。

五．材料拉伸和压缩时的力学性能

材料的力学性能—材料在外力作用下，其强度和变形方面所表现出来的性能（也称机械性能）。

    通过试验揭示材料在受力过程中所表现出的与试件几何尺寸无关的材料本身特性。如变形特性，破坏特性等。

    研究材料的力学性能的目的是确定在变形和破坏情况下的一些重要性能指标，以作为选用材料，计算构件强度、刚度的依据。

塑性材料:低碳钢等

脆性材料:铸铁等

    本节主要介绍低碳钢和铸铁在常温(指室温)、静载(指加载速度缓慢平稳)下的力学性能。

1.试件和设备

　标准试件:圆截面试件，标距L与直径d的比例分为，L=10d，L=5d；

　试验设备:拉力机 简图 实验

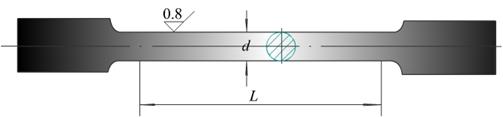
2.低碳钢拉伸时的力学性能

低碳钢是指含碳量在0.3%以下的碳素钢，如A3钢、16Mn钢。

拉伸试验（The Tensile Test）：绘出　F-△L 曲线（载荷——变形）

    由于F-△L 曲线与试样的尺寸有关，为了消除试件尺寸的影响，常采用应力应变曲线，即s-e曲线来代替F-△L曲线。

s-e曲线：

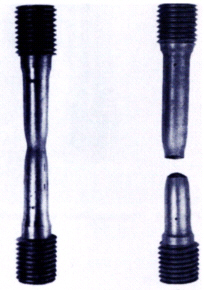
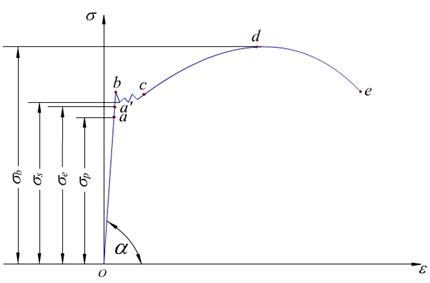
低碳钢试件拉伸时的s-e曲线

．弹性阶段比例极限σ_p

oa段：在拉伸的初始阶段应力s与应变e为直线关系直至a点，

此时a点所对应的应力值称为比例极限，用s_p表示。 

虎克定律

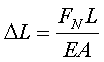
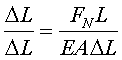
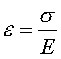
当s<s_p，有

　它表示应力与应变成正比，即有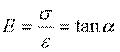

E为弹性模量

aa′段，已不再是直线，说明材料已不符合虎克定律。但在aa′段内卸载，变形也随之消失，说明aa′段也发生弹性变形，

oa′段称为弹性阶段。a′点所对应的应力值记作——弹性极限

弹性极限与比例极限非常接近，近似地用比例极限代替弹性极限。

．屈服阶段 屈服点_s(屈服极限)

bc段：屈服——应力超过弹性极限后继续加载，会出现一种现象，即应力增加很少或不增加，应变会很快增加，这种现象称之。

屈服极限——开始发生屈服的点所对应的应力，又称屈服强度

    在屈服阶段应力不变而应变不断增加，材料似乎失去了抵抗变形的能力，因此产生了显著的塑性变形。——此时若卸载，应变不会完全消失，而存在残余变形，也称塑性变形。所以s_s是衡量材料强度的重要指标。

．强化阶段  抗拉强度

cd段：越过屈服阶段后，如要让试件继续变形，必须继续加载，材料似乎强化了，cd 段即强化阶段。

强度极限——应变强化阶段的最高点（d 点）所对应的应力。它表示材料所能承受的最大应力。 　　

．颈缩阶段 

过d点后，即应力达到强度极限后，试件局部发生剧烈收缩的现象，称为颈缩，进而试件内部出现裂纹，名义应力下跌，至e点试件断裂

变形过程：弹性阶段、屈服阶段、强化阶段、

重要指标：比例极限、弹性极限、屈服极限、强度极限

4．塑性指标

    试件拉断后，弹性变形消失，但塑性变形仍保留下来。工程上用试件拉断后遗留下来的变形表示材料的塑性指标。

(1) 伸长率

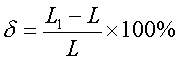
(2) 断面收缩率

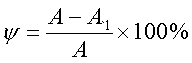
式中，L₁为试件拉断后的标距，L是原标距；A₁为试件断口处的最小横截面面积，A为原横截面面积。显然d、y 值越大，其塑性越好。

 d≥5％的材料称为塑性材料，如钢材、铜、铝等；

  d<5％的材料称为脆性材料，如铸铁、混凝土、石料等。

低碳钢压缩时的力学性能

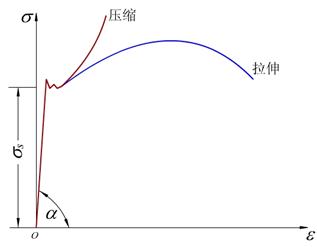
    认为低碳钢的抗拉性能与抗压性能是相同的。屈服阶段以后，试件会越压越扁，先是压成鼓形，最后变成饼状，故得不到压缩时的抗压强度。

其他塑性材料拉伸时的力学性能

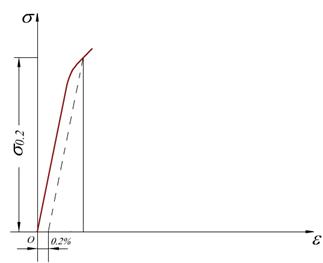
    对于没有明显屈服阶段的塑性材料，常用其产生0.2%塑性应变所对应的应力值作为名义屈服点，称为屈服强度，用 s_0.2表示。

铸铁拉(压)时的力学性能

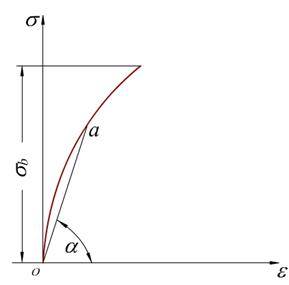
铸铁拉伸

．抗拉强度

    曲线没有明显的直线部分和屈服阶段，无缩颈现象而发生断裂破坏，塑性变形很小。把断裂时曲线最高点所对应的应力值记作s_b ，称为抗拉强度。铸铁的抗拉强度较低。

    由于铸铁总是在较小的应力下工作，且变形很小，故可近似地认为符合虎克定律。通常在s-e 曲线上用割线oa近似地代替曲线oa，并以割线oa的斜率作为弹性模量E。

．抗压强度s_by 

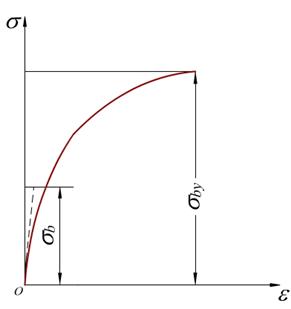
    曲线没有明显的直线部分，在应力较小时，可以近似地认为符合虎克定律。曲线没有屈服阶段，变形很小时沿与轴线大约成45°的斜截面发生破裂破坏。把曲线最高点的应力值称为抗压强度，用s_by 表示。 与拉伸时的 曲线(虚线)比较可见，铸铁材料的抗压强度约是抗拉强度的4～5倍。其抗压性能远好于抗拉性能，反映了脆性材料共有的属性。因此，工程中铸铁等脆性材料常用作受压构件，而不用作受拉构件。

常用工程材料的力学性能见表。

六．拉(压)杆的强度计算

许用应力和安全系数

任何工程材料能承受的应力都是有限度的。

极限应力——材料丧失正常工作能力时的应力。

塑性材料：当应力达到屈服点后，将发生明显的塑性变形，从而影响构件安全正常地工作，所以塑性变形是塑性材料破坏的标志。

极限应力:屈服强度s_s (或屈服强度s_0.2 )

脆性材料:没有明显的塑性变形，断裂是脆性材料破坏的标志。

极限应力:抗拉强度s_b 和抗压强度s_by 

构件的工作应力必须小于材料的极限应力。

许用应力[s]——构件安全工作时，材料允许承受的最大应力。

许用应力等于极限应力除以大于l的系数n

 塑性材料的安全系数取 1.2～2.5，脆性材料的安全系数取2.0～3.5。

强度计算

强度条件——最大工作应力不超过材料的许用应力。

强度计算——应用强度条件式计算

(1)校核强度   已知外力F、横截面积A和许用应力[s]，计算出最大工作应力，检验是否满足强度条件，从而判断构件是否能够安全可靠工作。                                              

(2)设计截面   已知外力F、许用应力[s]，由A≥F_N／[s]计算出截面面积A，然后根据工程要求的截面形状，设计出构件的截面尺寸。 

(3)确定许可载荷 已知构件的截面面积A、许用应力[s]，由F_Nmax≤A[s]计算出构件所能承受的最大内力F_Nmax，再根据内力与外力的关系，确定出构件允许的许可载荷值[F]。 

    工程实际中，进行构件的强度计算时，根据有关设计规范，最大工作应力若大于许用应力，但只要不超过许用应力的5%也是允许的。

例4-2 某铣床工作台进给油缸如图所示，缸内工作油压p＝2MPa，油缸内径D＝75mm，活塞杆直径d＝18mm，已知活塞杆材料的许用应力[s]＝50MPa，试校核活塞杆的强度。

解 （1）求活塞杆的轴力

（2）按强度条件校核

s<[s]