第七章  第五节  组合变形

一 、 弯曲与拉压组合变形的强度计算

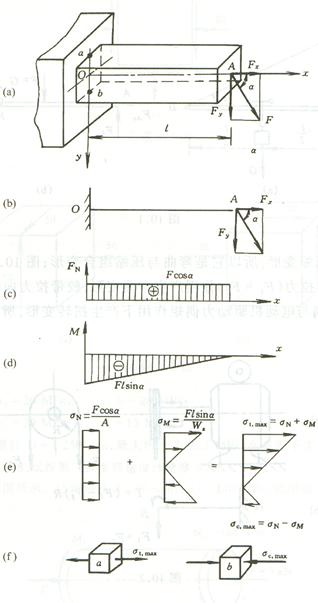
设矩形等截面悬臂梁如图 a 所示 , 外力F位于梁的纵向对称平面 Ozy 内 , 并与梁的轴线x成α角。将外力F分解为轴向力F_x=Fcosα和横向力 Fy=Fsinα。力 F_x使梁产生拉伸变形 ,力Fy使梁产生平面弯曲,所以梁产生弯曲与拉伸的组合变形。画出梁的轴力图和弯矩图（图c.d） 。由图可知，危险截面在悬臂梁的根部（O截面），截面ｏ上的应力分布如图e所示。 它由轴力 F_N=Fcosα引起的正应力σ_N= 和弯矩Ｍ引起的正应力σ_M= 叠加而得。从截面ｏ的应力分布可以看出 ,上、下边缘各点为危险点( 如图 1a 中的 a,b 点 ), 且均处于单向应力状态 ( 图 f)。

对抗拉与抗压性能相同的塑性材料 , 当发生弯曲与拉伸组合变形时 , 从图 a、e  中可以看出,对抗拉与抗压性能相同的塑性材料 , 当发生弯曲与拉伸组合变形时 , 最大拉应力发生在 ｏ 截 面的上边缘 ; 当发生弯曲与压缩组合变形时 , 最大压应力 , 发生在 ｏ 截面的下边缘。强度条件可 写成统一的式子 , 即

对于抗拉与抗压性能不相同的脆性材料 , 可根据危险截面上、下边缘应力分布的实际情况 ,按上述方法分别进行计算。

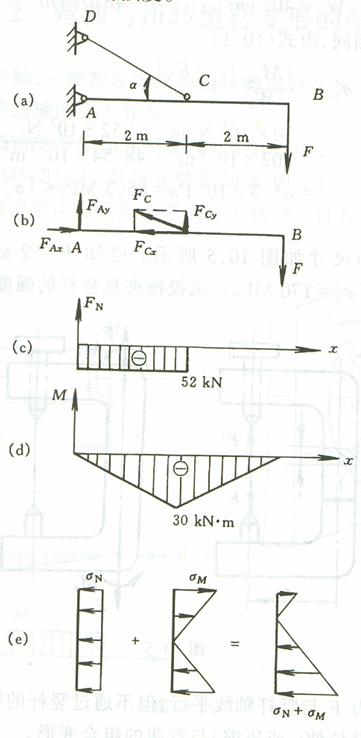
例 1 简易悬臂吊车如图 a 所示 , 起吊重力 F=15KN, α=30 。横梁 AB 为 No.25a工字钢 ,[ σ ]=100MPa, 试校核梁 AB 的强度。

解 (1) 对梁 AB 进行受力分析 ( 图 b)。 先求约束力 ,

 由∑M_A(F)=0,

—F × 4m＋Fcsinα× 2m=0

得   Fc=4F=4×15 kN=60Kn.

F_cx=FcCOSα=60COS30⁰=52Kn.

Fcy=Fcsinα=60sin30⁰ =30Kn.

∑F_X =0    F_AX =F_CX =52kN.

∑Fy=0    F_Ay + Fcy-F=0.

F_{A y}=F- Fcy=-5kN.

梁 AB 承受弯曲与压缩组合变形。

(2) 画出梁 AB 的内力图如图 c,d 所示。梁 AB 上截面 C 左侧为危险截面。

(3) 校核梁 AB 的强度     由附录型钢表查得 No.25a 工字钢

Wz=402CM³,   A=48.54CM²

因钢材抗拉与抗压强度相同 ,

 所以    

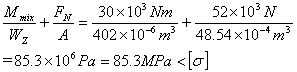
故梁 AB 满足强度条件。

二、梁弯曲时的强度条件及计算

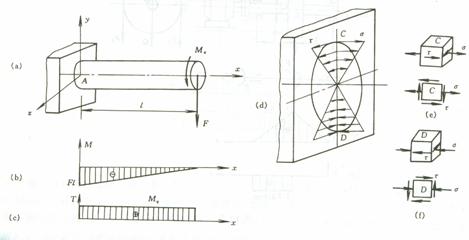
工程上机械传动中的转轴 ,一般都在弯曲与扭转的组合变形下工作 , 如图所示电动机转轴等。现讨论弯曲与扭转圆轴的应力分布。

画出弯扭组合变形的圆轴的弯矩图和扭矩图 ( 图 b,c)。由此可以分析 , 在危险截面 A 上必然存在弯曲正应力和扭转切应力 , 其分布情况如图 d 所示 ,C ,D 两点为危险点。取原始单元体 ( 图 e ,f), 危险点的应力状态为平面应力状态。且有

一般转轴由塑性材料制成 , 故按第三强度理论和第四强度理论的强度条件 :

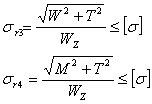
   需要强调的是 ,上面两式只适用于塑性材料制成的圆轴 ( 包括空心圆轴 ) 在弯曲与扭转组合变形时的强度计算 。

例 2 ：图 10.7a 所示传动轴 AB 由电机带动 , 轴长 J =1.2m, 在跨中央安装一胶带轮 , 重力 G =5kN, 半径 R=0.6m, 胶带紧边张力 F₁=6kN, 松边张力 F₂=3kN 。轴直径 d =0.1m, 材料许用应力 [ σ ]=50MPa. 试按第三强度理论校核轴的强度。

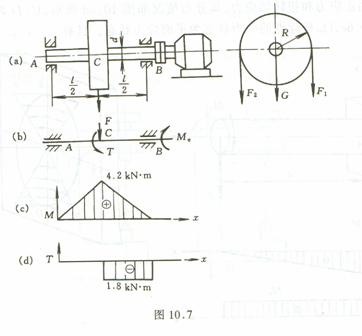
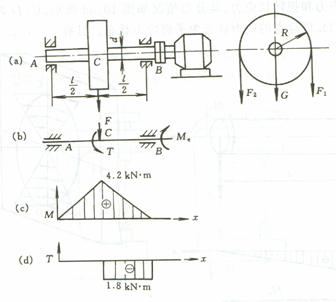
分析后，由学生解，再分析。