第七章  第四节 直梁的弯曲

一．直梁平面弯曲的概念

弯曲变形：杆件在垂直于其轴线的载荷作用下，使原为直线的轴线变为曲线的变形。

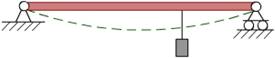
梁——以弯曲变形为主的直杆称为直梁，简称梁。

梁的计算简图

载荷：（1）集中力　（2）集中力偶　（3）分布载荷

梁的类型

(1)简支梁　

(2)外伸梁

(3)悬臂梁

二．梁弯曲时的内力

1．梁弯曲时横截面上的内力——剪力和弯矩

问题：任截面处有何内力？

• 该内力正负如何规定？

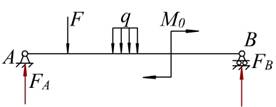
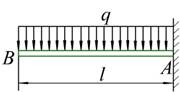
例7－1　图示的悬臂梁AB，长为l ，受均布载荷q 的作用，求梁各横截面上的内力。

求内力的方法——截面法

截面法的核心——截开、代替、平衡   内力与外力平衡

解：为了显示任一横截面上的内力，假想在距梁的左端为x处沿m-m截

面将梁切开。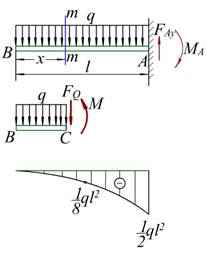

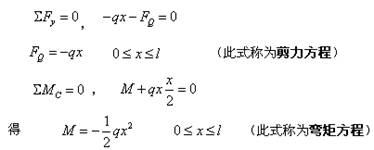
由剪力方程和弯矩方程，代入相应数据可以求得梁各横截面上的内力——剪力和弯矩。

    梁发生弯曲变形时，横截面上同时存在着两种内力。

剪力——作用线切于截面、通过截面形心并在纵向对称面内。

弯矩——位于纵向对称面内。

剪切弯曲——横截面上既有剪力又有弯矩的弯曲。

纯弯曲——梁的横截面上只有弯矩而没有剪力。

    工程上一般梁（跨度L与横截面高度h 之比L/h＞5），其剪力对强度和刚度的影响很小，可忽略不计，故只需考虑弯矩的影响而近似地作为纯弯曲处理。

规定：使梁弯曲成上凹下凸的形状时，则弯矩为正；反之使梁弯曲成下凹上凸形状时，弯矩为负，

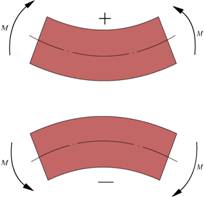
2．弯矩图

弯矩图：以与梁轴线平行的坐标x表示横截面位置，纵坐标y按一定比例表示各截面上相应弯矩的大小。

例7－2　试作出例7－1中悬臂梁的弯矩图。

解 （1）建立弯矩方程 由例7－1知弯矩方程为

（2）画弯矩图

    弯矩方程为一元二次方程，其图象为抛物线。求出其极值点相连便可近似作出其弯矩图。

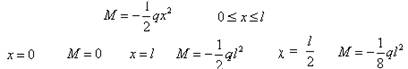
例7－3　图示的简支梁AB，在C点处受到集中力F作用，尺寸a 、b 和l 均为已知，试作出梁的弯矩图。

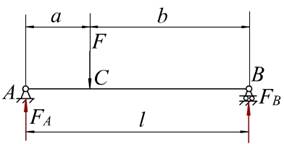
解 （1）求约束反力

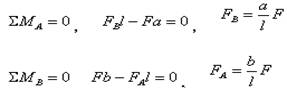
（2）建立弯矩方程 上例中梁受连续均布载荷作用，各横截面上的弯矩为x的一个连续函数，故弯矩可用一个方程来表达，而本例在梁的C点处有集中力F作用，所以梁应分成AC和BC两段分别建立弯矩方程。

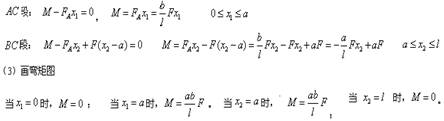
例7－4　图示的简支梁AB，在C点处受到集中力偶M₀作用，尺寸a 、b 和l 均为已知，试作出梁的弯矩图。

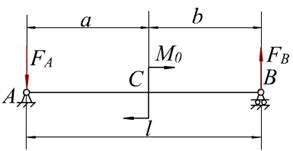
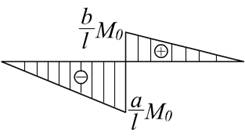
总结上面例题，可以得到作弯矩图的几点规律：

（1）梁受集中力或集中力偶作用时，弯矩图为直线，并且在集中力作用处，弯矩发生转折；在集中力偶作用处，弯矩发生突变，突变量为集中力偶的大小。

（2）梁受到均布载荷作用时，弯矩图为抛物线，且抛物线的开口方向与均布载荷的方向一致。

（3）梁的两端点若无集中力偶作用，则端点处的弯矩为0；若有集中力偶作用时，则弯矩为集中力偶的大小。

三． 剪力图与弯矩图

弯矩图：（1）梁受集中力或集中力偶作用时，弯矩图为直线，并且在集中力作用处，弯矩发生转折；

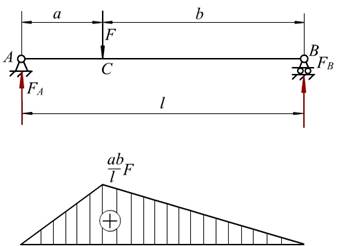
在集中力偶作用处，弯矩发生突变，突变量为集中力偶的大小 。

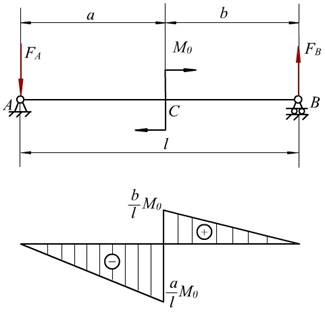
　（2）梁受到均布载荷作用时，弯矩图为抛物线，且抛物线的开口方向与均布载荷的方向一致。

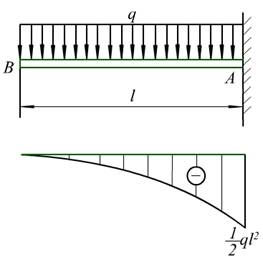
（3）梁的两端点若无集中力偶作用，则端点处的弯矩为0；若有集中力偶作用时，则弯矩为集中力偶的大小。

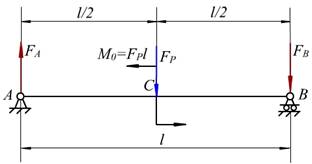
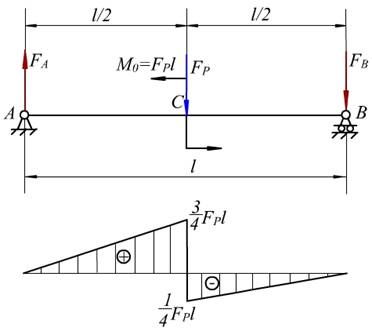
例7－5　图示简支梁，受集中力F_P 和集中力偶M₀=F_Pl 作用，试作此梁的弯矩图。 

例

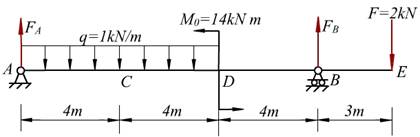
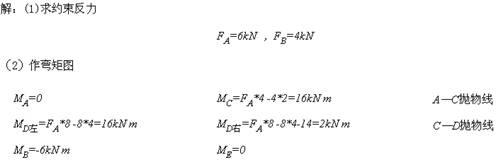
总结上面例题，可以得到作弯矩图的几点规律：

（1）梁受集中力或集中力偶作用时，弯矩图为直线，并且在集中力作用处，弯矩发生转折；在集中力偶作用处，弯矩发生突变，突变量为集中力偶的大小。

（2）梁受到均布载荷作用时，弯矩图为抛物线，且抛物线的开口方向与均布载荷的方向一致。

（3）梁的两端点若无集中力偶作用，则端点处的弯矩为0；若有集中力偶作用时，则弯矩为集中力偶的大小。

四 梁纯弯曲时的强度条件

1．梁纯弯曲的概念

纯弯曲——梁的横截面上只有弯矩而没有剪力。

Q = 0，M = 常数。

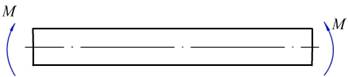
2．梁纯弯曲时横截面上的正应力

．梁纯弯曲时的变形特点

平面假设：

1）变形前为平面变形后仍为平面 

2）始终垂直与轴线 

中性层：既不缩短也不伸长（不受压不受拉）。

中性层是梁上拉伸区与压缩区的分界面。

中性轴：中性层与横截面的交线

变形时横截面是绕中性轴旋转的。

．梁纯弯曲时横截面上正应力的分布规律 

纯弯曲时梁横截面上只有正应力而无切应力。

    由于梁横截面保持平面，所以沿横截面高度方向纵向纤维从缩短到伸长是线性变化的，因此横截面上的正应力沿横截面高度方向也是线性分布的。  以中性轴为界，凹边是压应力，使梁缩短，凸边是拉应力，使梁伸长，横截面上同一高度各点的正应力相等，距中性轴最远点有最大拉应力和最大压应力，中性轴上各点正应力为零。

．梁纯弯曲时正应力计算公式 

在弹性范围内，经推导可得梁纯弯曲时横截面上任意一点的正应力为           

式中， M为作用在该截面上的弯矩（Nmm）； y为计算点到中性轴的距离（mm）；为横截面对中性轴z的惯性矩（mm⁴）。

在中性轴上 y=0，所以s=0 ；当y=y_max 时，s=s_max 。最大正应力产生在离中性轴最远的边缘处，

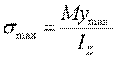    或    

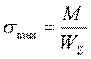
__横截面对中性轴z的抗弯截面模量(mm³)

    计算时， M和y均以绝对值代入，至于弯曲正应力是拉应力还是压应力，则由欲求应力的点处于受拉侧还是受压侧来判断。受拉侧的弯曲正应力为正，受压侧的为负。

    弯曲正应力计算式虽然是在纯弯曲的情况下导出的，但对于剪切弯曲的梁，只要其跨度L与横截面高度h之比L/h ＞5，仍可运用这些公式计算弯曲正应力。

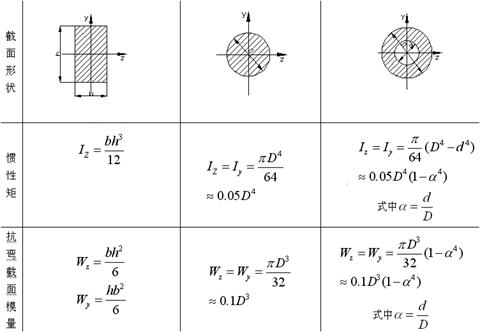
3．惯性矩和抗弯截面模量

简单截面的惯性矩和抗弯截面模量计算公式

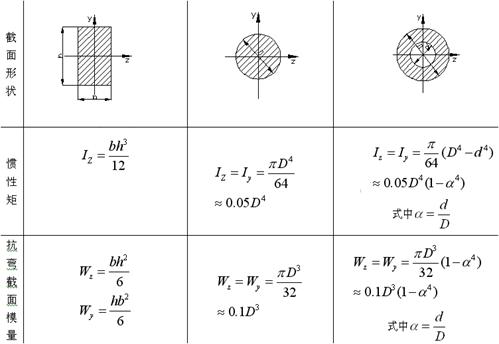
4．梁纯弯曲时的强度条件

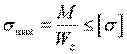
对于等截面梁，弯矩最大的截面就是危险截面，其上、下边缘各点的弯曲正应力即为最大工作应力，具有最大工作应力的点一般称为危险点。

梁的弯曲强度条件是：梁内危险点的工作应力不超过材料的许用应力。 运用梁的弯曲强度条件，可对梁进行强度校核、设计截面和确定许可载荷。

例7－6　在例7－3中的简支梁，若选用D=100mm，d=60mm的空心圆形截面钢制造，已知梁的跨度l=3m，a=1m，b=2m，集中载荷F=25kN，许用正应力[s]=200MPa。 不计梁的自重，试校核该梁的强度。 

五 纯弯曲时梁的正应力

　　在平面弯曲时，工程上近似地认为梁横截面上的弯矩是由截面上的正应力形成的，而剪力则由截面上的切应力所形成。本章将在梁弯曲时的内力分析的基础上，导出梁弯曲时的应力与变形的计算，建立梁的强度和刚度条件。

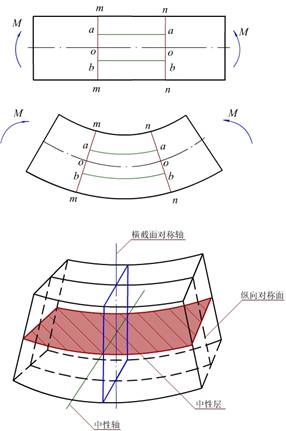
　　为了研究梁横截面上的正应力分布规律，取一矩形截面等直梁，在表面画些平行于梁轴线的纵线和垂直干梁轴线的横线。在梁的两端施加一对位于梁纵向对称面内的力偶，梁则发生弯曲。梁任意横截面上的内力只有弯矩而无剪力，这种弯曲称为纯弯曲，这种梁称为纯弯曲梁。

　　通常从变形的几何关系、物理关系和静力平衡条件三个方面来推导出纯弯曲梁横截面上的正应力公式。

1、实验观察

梁发生弯曲变形后，我们可以观察到以下现象：

1、横向线仍是直线且仍与梁的轴线正交，只是相互倾斜了一个角度

　　2、纵向线（包括轴线）都变成了弧线。

　　3、梁横截面的宽度发生了微小变形，

　　根据上述现象，可对梁的变形提出如下假设：

　　① 平面假设：梁弯曲变形时，其横截面仍保持平面，且绕某轴转过了一个微小的角度。

　　② 单向受力假设：设梁由无数纵向纤维组成，则这些纤维处于单向受拉或单向受压状态。

　　可以看出，梁下部的纵向纤维受拉伸长，上部的纵向纤维受压缩短，其间必有一层纤维既不伸长也木缩短，这层纤维称为中性层。中性层和横截面的交线称为中性轴，即图中的Z轴。梁的横截面绕Z轴转动一个微小角度。

2、变形的几何关系

　　图中梁的两个横截面之间距离为dx，变形后中性层纤维长度仍为dx且dx=ρdθ。距中性层为y的某一纵向纤维的线应变ε为：

　　即梁内任一纵向纤维的线应变ε与它到中性层的距离y成正比。
    3、变形的物理关系

　　由单向受力假设，当正应力不超过材料的比例极限时，将虎克定律代入上式，得：

可见矩形截面梁在纯弯曲时的正应力的分布有如下特点：
　　 ① 中性轴上的线应变为零，所以其正应力亦为零。
　　 ② 到中性轴距离相等的各点，其线应变相等。根据虎克定律，它们的正应力也相等。
　　 ③ 在图示的受力情况下，中性轴上部各点正应力为负值，中性轴下部各点正应力为正值。
　　 ④ 正应力沿y轴线性分布。最大正应力（绝对值）在离中性轴最

4、梁纯弯曲时横截面上正应力的分布规律 

5、纯弯曲时梁横截面上只有正应力而无切应力。

    由于梁横截面保持平面，所以沿横截面高度方向纵向纤维从缩短到伸长是线性变化的，因此横截面上的正应力沿横截面高度方向也是线性分布的。

    以中性轴为界，凹边是压应力，使梁缩短，凸边是拉应力，使梁伸长，横截面上同一高度各点的正应力相等，距中性轴最远点有最大拉应力和最大压应力，中性轴上各点正应力为零。

6、梁纯弯曲时正应力计算公式 

在弹性范围内，经推导可得梁纯弯曲时横截面上任意一点的正应力为

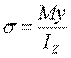      式中， M为作用在该截面上的弯矩（Nmm）； y为计算点到中性轴的距离（mm）； I为横截面对中性轴z的惯性矩（mm⁴）。

    在中性轴上 y=0，所以s=0 ；当y=y_max 时，s=s_max 。最大正应力产生在离中性轴最远的边缘处，

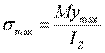
或

__________横截面对中性轴z的抗弯截面模量mm³)

    计算时， M和y均以绝对值代入，至于弯曲正应力是拉应力还是压应力，则由欲求应力的点处于受拉侧还是受压侧来判断。受拉侧的弯曲正应力为正，受压侧的为负。

    弯曲正应力计算式虽然是在纯弯曲的情况下导出的，但对于剪切弯曲的梁，只要其跨度L与横截面高度h之比L/h ＞5，仍可运用这些公式计算弯曲正应力。

惯性矩和抗弯截面模量

简单截面的惯性矩和抗弯截面模量计算公式

梁纯弯曲时的强度条件

对于等截面梁，弯矩最大的截面就是危险截面，其上、下边缘各点的弯曲正应力即为最大工作应力，具有最大工作应力的点一般称为危险点。

梁的弯曲强度条件是：梁内危险点的工作应力不超过材料的许用应力。 运用梁的弯曲强度条件，可对梁进行强度校核、设计截面和确定许可载荷。

例7－6　在例7－3中的简支梁，若选用D=100mm，d=60mm的空心圆形截面钢制造，已知梁的跨度l=3m，a=1m，b=2m，集中载荷F=25kN，许用正应力[s]=200MPa。 不计梁的自重，试校核该梁的强度。 

六．梁纯弯曲时的强度条件

梁纯弯曲的概念

纯弯曲——梁的横截面上只有弯矩而没有剪力。

Q = 0，M = 常数。

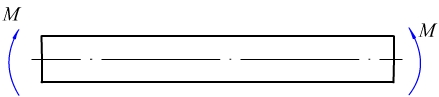
梁纯弯曲时横截面上的正应力

1．梁纯弯曲时的变形特点

平面假设：

1）变形前为平面变形后仍为平面 

2）始终垂直与轴线 

中性层：既不缩短也不伸长（不受压不受拉）。

中性层是梁上拉伸区与压缩区的分界面。

中性轴：中性层与横截面的交线。

变形时横截面是绕中性轴旋转的。

2．梁纯弯曲时横截面上正应力的分布规律 

纯弯曲时梁横截面上只有正应力而无切应力。

    由于梁横截面保持平面，所以沿横截面高度方向纵向纤维从缩短到伸长是线性变化的，因此横截面上的正应力沿横截面高度方向也是线性分布的。

    以中性轴为界，凹边是压应力，使梁缩短，凸边是拉应力，使梁伸长，横截面上同一高度各点的正应力相等，距中性轴最远点有最大拉应力和最大压应力，中性轴上各点正应力为零。

3．梁纯弯曲时正应力计算公式 

在弹性范围内，经推导可得梁纯弯曲时横截面上任意一点的正应力为

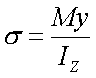
式中， M为作用在该截面上的弯矩（Nmm）； y为计算点到中性轴的距离（mm）； I为横截面对中性轴z的惯性矩（mm⁴）。

    在中性轴上 y=0，所以s=0 ；当y=y_max 时，s=s_max 。最大正应力产生在离中性轴最远的边缘处，

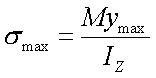
或

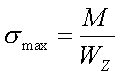
__________横截面对中性轴z的抗弯截面模量(mm³)

    计算时， M和y均以绝对值代入，至于弯曲正应力是拉应力还是压应力，则由欲求应力的点处于受拉侧还是受压侧来判断。受拉侧的弯曲正应力为正，受压侧的为负。

    弯曲正应力计算式虽然是在纯弯曲的情况下导出的，但对于剪切弯曲的梁，只要其跨度L与横截面高度h之比L/h ＞5，仍可运用这些公式计算弯曲正应力。

惯性矩和抗弯截面模量

简单截面的惯性矩和抗弯截面模量计算公式

梁纯弯曲时的强度条件

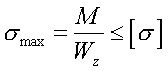
对于等截面梁，弯矩最大的截面就是危险截面，其上、下边缘各点的弯曲正应力即为最大工作应力，具有最大工作应力的点一般称为危险点。

梁的弯曲强度条件是：梁内危险点的工作应力不超过材料的许用应力。 运用梁的弯曲强度条件，可对梁进行强度校核、设计截面和确定许可载荷。

例7－6　在例7－3中的简支梁，若选用D=100mm，d=60mm的空心圆形截面钢制造，已知梁的跨度l=3m，a=1m，b=2m，集中载荷F=25kN，许用正应力[s]=200MPa。 不计梁的自重，试校核该梁的强度。 

七 提高梁强度的主要措施

    提高梁强度的主要措施是：

1）降低弯矩M的数值 2)增大抗弯截面模量W_z的数值

降低最大弯矩M_max数值的措施

1）．合理安排梁的支承

最大弯矩，只为前者的五分之一。

2）．合理布置载荷

2、合理选择梁的截面

    合理的截面应该是:用最小的截面面积（即用材料少），得到大的抗弯截面模量W_z

1）．形状和面积相同的截面，采用不同的放置方式，则W_z值可能不相同

    竖放时（左）抗弯截面模量大，承载能力强，不易弯曲；

    平放时（右），抗弯截面模量小，承载能力差，易弯曲。

    工字钢、槽钢等梁放置方式不同其抗弯截面模量也不同，承载能力不同。

2）．面积相等而形状不同的截面，其抗弯截面模量W_z值不相同

    材料远离中性轴的截面（如圆环形、工字形等）比较经济合理。

       对于矩形截面，则可把中性轴附近的材料移置到上、下边缘处而形成工字形截面。

    工程中的吊车梁、桥梁常采用工字形、槽形或箱形截面，房屋建筑中的楼板采用空心圆孔板。

3）．截面形状应与材料特性相适应

    对抗拉和抗压强度相等的塑性材料，宜采用中性轴对称的截面，如圆形、矩形、工字形等。

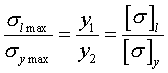
对抗拉强度小于抗压强度的脆性材料，宜采用中性轴偏向受拉一侧的截面形状。

3、采用等强度梁

    对于等截面梁，除M_max所在截面的最大正应力达到材料的许用应力外，其余截面的应力均小于，甚至远小于许用应力。

    为了节省材料，减轻结构的重量，可在弯矩较小处采用较小的截面，这种截面尺寸沿梁轴线变化的梁称为变截面梁。

等强度梁——使变截面梁每个截面上的最大正应力都等于材料的许用应力，则这种梁称之。

例：

八 梁弯曲时的变形和刚度条件

1、梁弯曲时的变形

挠曲线：AB₁

挠度：y_C(CC₁)     y_B(BB₁)      形心

    正、负号规定：与坐标轴y的正方向一致时为正；反之为负。单位mm

转角：横截面相对于原来位置转过的角度q。单位弧度

    正、负号规定：逆时针方向的转角为正，反之为负。

2、梁弯曲时的刚度条件