一、渐开线的形成及基本性质

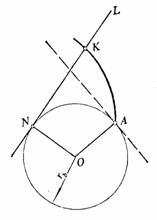
如图所示，一直线L与半径为r_b的圆相切，当直线沿该圆作纯滚动时，直线上任一点的轨迹即为该圆的渐开线。这个圆称为渐开线的基圆，而作纯滚动的直线L称为渐开线的发生线。

      

渐开线的形成图   基圆大小与渐开线形状的关系

由渐开线的形成可知，它有以下性质：

（1）发生线在基圆上滚过的一段长度等于基圆上相应被滚过的一段弧长，即

（2）因N点是发生线沿基圆滚动时的速度瞬心，故发生线KN是渐开线K点的法线。又因发生线始终与基圆相切，所以渐开线上任一点的法线必与基圆相切。

（3）发生线与基圆的切点N即为渐开线上K点的曲率中心，线段为K点的曲率半径。随着K点离基圆愈远，相应的曲率半径愈大；而K点离基圆愈近，相应的曲率半径愈小。

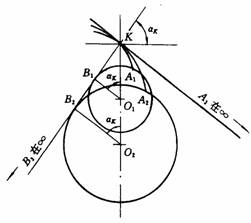
（4）渐开线的形状取决于基圆的大小。如图7-4所示，基圆半径愈小，渐开线愈弯曲；基圆半径愈大，渐开线愈趋平直。当基圆半径趋于无穷大时，渐开线便成为直线。所以渐开线齿条（直径为无穷大的齿轮）具有直线齿廓。

（5）渐开线是从基圆开始向外逐渐展开的，故基圆以内无渐开线。

二、渐开线函数

  渐开线上K点的极坐标，可用r_k与θ_k表示，r_k为K点的向径，θ_k为渐开线在K点的展角

     θ_k=invα_k=tgα_k-α_k

上式中θ_k=invα_k又称为渐开线函数。

二、渐开线齿廓满足齿廓啮合基本定律（或者说满足定传动比要求）

   

    常数   式（1）

三、渐开线齿廓啮合的特点

1、渐开线齿廓啮合的啮合线是直线——N₁N₂啮合点的轨迹

啮合线、公法线、两基圆的内公切线三线重合。

2、渐开线齿廓啮合的啮合角不变

：N₁N₂与节圆公切线之间的夹角

=渐开线在节点处啮合的压力角

3、渐开线齿廓啮合具有可分性。

式（1）表明，i₁₂决定于基圆大小

（这一特点对渐开线齿轮的制造、安装都是十分有利的）。

　

上一节

下一节