一、锥齿轮传动的特点

圆锥齿轮用于相交两轴之间的传动，其中应用最广泛的是两轴交角S=d₁+d₂=90°的直齿圆锥齿轮。

   锥齿轮的齿轮有直齿、斜齿和曲齿等多种形式。

二、锥齿轮的当量齿轮和当量齿数

  当发生面A沿基圆锥作纯滚动时，平面上一条通过锥顶的直线OK将形成一渐开线曲面，此曲面即为直齿圆锥齿轮的齿廓曲面，直线OK上各点的轨迹都是渐开线。渐开线NK上各点与锥顶O的距离均相等，所以该渐开线必在一个以O为球心，OK为半径的球面上，因此圆锥齿轮的齿廓曲线理论上是以锥顶O为球心的球面渐开线。但因球面渐开线无法在平面上展开，给设计和制造造成困难，故常用背锥上的齿廓曲线来代替球面渐开线。

将扇形齿轮补足为完整的圆柱齿轮，这个圆柱齿轮称为圆锥齿轮的当量齿轮，当量齿轮的齿数z_v称为当量齿数。由图可见

而，故                     

因δ总是大于零度，故z_v＞z，且往往不是整数。

综上所述，一对圆锥齿轮的啮合相当于一对当量圆柱齿轮的啮合，因此可把圆柱齿轮的啮合原理运用到圆锥齿轮。

三、锥齿轮的参数和几何尺寸计算

按GB12369—1990规定，直齿圆锥齿轮传动的几何尺寸计算是以其大端为标准。当轴交角Σ=90°时。

       

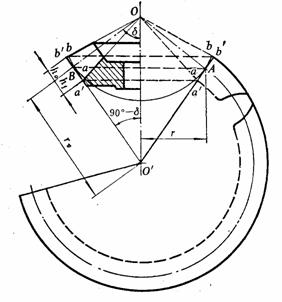
         图    圆锥齿轮的背锥和当量齿数

四、锥齿轮传动的受力分析

 

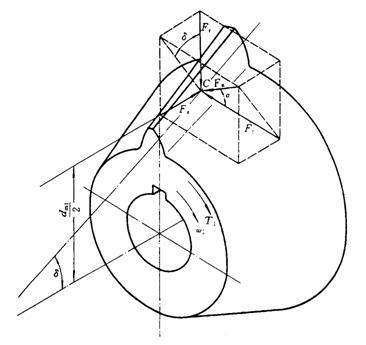
       图   直齿圆锥齿轮受力分析

 

图为直齿圆锥齿轮轮齿受力情况。由于圆锥齿轮的轮齿厚度和高度向锥顶方向逐渐减小，故轮齿各剖面上的弯曲强度都不相同，为简化起见，通常假定载荷集中作用在齿宽中部的节点上。法向力F_n可分解为三个分力：

圆周力

F_t=                       

径向力

F_r=F_t tanacosd                  

轴向力

F_a= F_t tanasind                

式中d_m1为小齿轮齿宽中点的分度圆直径，d_m1=d₁-bsind₁

圆周力F_t和径向力F_r的方向判断与直齿圆柱齿轮相同。轴向力F_a的方向对两个齿轮都是背着锥顶。当两轴夹角Σ=90°时，因sind₁=cosd₂，cosd₁=sind₂，故

F_r1=-F_a2                          

F_a1=-F_r2                                             

F_t1=-F_t2   

　

上一节

下一节