直齿圆柱齿轮传动的作用力及计算载荷

齿面接触线上的法向载荷Fn——名义载荷（未计及载荷波动，载荷沿齿宽方向的不均匀性和轮齿齿廓曲线误差等）

计算载荷；Fnc=KFn

载荷系数：K= 、、、

 ——工作情况系数    ——初载荷系数

——齿向载荷分布系数   ——齿间载荷分配系数

　

1、工作情况系数K_A

考虑了齿轮啮合时，外部因素引起的附加动载荷对传动的影响，表8-2所示

它与原动机与工作机的类型与特性，联轴器类型等有关

2、动载荷系数K_V——考虑齿轮制造误差和装配误差及弹性变形等内部因素引起的附加动载荷的影响

主要影响因素：1）齿轮的制造精度Pb₁≠Pb₂  2）圆周速度V，图8-9

a）当P_b2>P_b1时（图8-7）后一对齿轮未进入啮合区就开始接触，产生动载荷（∵此时过接触点作齿廓的公法线与连心线交点P’(节点)与P不重合，这样使实际的）→措施：从动轮2齿顶修缘，使齿轮2在齿顶处P'_b2<P_b2，使开始啮合时轮齿法向基节小一些，减小动载

b）当P_b1>P_b2时；如图8-8，则前一对齿将脱开啮合时，后一对齿虽已进入啮合区，但尚未接触，而要待前一对齿离开正确啮合区一段距离后，后一对齿才开始啮合→产生齿腰（中间）冲击→措施：主动轮1齿顶修缘（虚线齿廓），延长一对齿的啮合时间

降低K_V措施：1）提高齿轮制造安装精度；2）减小V（减小齿轮直径d）；3）齿顶修缘

注意：修缘要适当，过大则重合度下降过大。

一般高速齿轮和硬齿面齿轮应进行修缘，但修缘量与修缘的曲线确定则比较复杂。

3、齿向载荷分布系数——考虑轴的弯曲、扭转变形、轴承、支座弹性变形及制造和装配误差而引起的沿齿宽方向载荷分布不均匀的影响。如图9-11所示

影响因素：1）支承情况：对称布置，好；非对称布置↓；悬臂布置，差。

2）齿轮宽度b  b↑  ↑。

3）齿面硬度，硬度越高，赵易偏载，齿面较软时有变形退让。

4）制造、安装精度——精度越高，越小。

减小措施：1）提高制造安装精度；2）提高支承刚度，尽量避免悬臂布置；3）采用鼓形齿（如图8-2）；4）螺旋角修形——沿小齿轮齿宽进行修形，以补偿由于轴的弯曲和扭转变形引起的啮合线位置的改变。

 分：

1）——用于齿面接触疲劳强度计算，表8-3，与精度等级、齿面硬度、支承布置有关，齿宽系数，=b/d

2）——用于齿根变曲疲劳强度计算，按和b/h之比值，查图8-13。

b—齿宽，h—齿高。

4、齿间载荷分配系数——考虑同时有多对齿啮合时各对轮齿间载荷分配不均匀的系数。

影响因素：啮合刚度，基圆齿距误差（P_b），修缘量，跑合程度等。

分：

1）——齿面接触疲劳强度计算用

2）——齿根弯曲疲劳强度计算用    表8-4

　

直齿圆柱齿轮传动的强度计算

一、轮齿的受力分析

忽略摩擦力，法向力F_n沿啮合线作用于节点处（将分布力简化为集中力）F_n与过节点P的圆周切向成角度。F_n可分解为F_t和F_r

1、力的大小

圆周力  F_t=2π/d₁    F_t1=-F_t2

径向力  F_r=F_t/tgα    F_r1=-F_r2      大小相等，方向相反

法向力  F_n=F_t/cosα   F_n1=-F_n2

T₁——小齿轮上传递的扭矩（N.mm）  d₁——小齿轮上的直径（mm）, α=20°

2、力的方向

F_t——“主反从同”，F_r——指向轴线—外齿轮

                        背向轴线—内齿轮

二、齿根弯曲疲劳强度计算——防止弯曲疲劳折断

由于轮齿啮合时，啮合点的位置从齿顶到齿根不断变化，且轮齿啮合时也是由单对齿到两对齿之间变化，由此，齿根部分的弯曲应力是在不断变化，最大弯曲应力产生在单齿对啮合区的最高点。但计算比较复杂。

计算假设：1）单齿对啮合；2）载荷作用于齿顶；3）计算模型为悬臂梁；4）用重合度系数考虑齿顶啮合时非单齿对啮合影响；5）只考虑弯曲应力，∵裂纹首先在受拉侧产生，且压应力对较小对拉应力有抵消作用；6）危险截面——30°切线法定

——齿顶压力角

→弯曲拉应力；——产生压应力

如图8-16，齿根危险截面的弯曲应力是为：

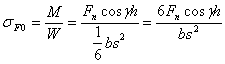
计入载荷系数K，代入上式

——Y_Fa

∴

Y_Fa——齿形系数，只与齿形有关，即与，C*，Z₁，X，有关，当，C*一定时，只与Z₁，X，有关，而与m无关。Y_Fa——表8-5

另计入：应力修正系数Y_Sa——考虑齿根圆角引起的应力集中和其它应力的影响，表9-5

       重合度系数Y_ε——考虑非单齿对啮合的影响

∴弯曲疲劳强度的校核公式：

  Mpa  (8-4)

其中，Y_ε=0.25+0.75/          ——端面重合度

令——齿宽系数（设计时选定），将和，代入上式得

校核公式：   Mpa           (8-5a)

设计公式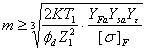： （mm）取标准值  （8-5b）

三、齿面接触疲劳强度计算——防止疲劳点蚀

要求齿面的最大接触应力不超过接触疲劳极限应力 

计算依据：赫其公式（弹性力学）——式（8-44）

即齿面最大接触应力  

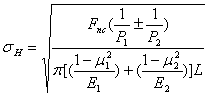
L——接触线长度

令，——啮合点齿廓综合曲率半径：+—外啮合；-—内啮合。

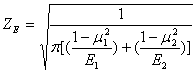——弹性影响系数与配对齿轮材料有关，见表8-6

∴

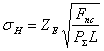
强度条件 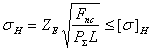   ，  Mpa      (8-6)

问题是如何定，L？  ∵

计算点——理论上为小齿轮单齿对啮合区内（最小处）的最低点，图8-17C点，另大轮单齿对啮合最低点D点也较大。但计算较为复杂，且实际上节点处接触应力也较大，而点蚀又往往是从靠近节线附近（齿根部位）首先产生。

∵实际计算点——节点（单齿对），即将节点处齿廓的啮合看成是以节点处齿廓曲率半径为半径的两个圆柱体相接触。如图8-17所示。

如图8-17，在节点P处：

，

∴

∵  （齿数比）

∴

∴

∵  ∴实际啮合时，并不总是单齿对啮合，∴实际接触线长度由齿宽b和端面重合度决定

实际接触线长度（考虑b与）

    ——重合度系数    （8-7b）

将、L及代入式（8-6）得

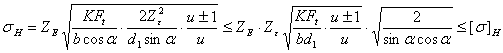
令——节点区域系数

则得接触疲劳强度的校核公式：

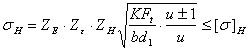    Mpa          (8-8)

引入齿宽系数，则得（）

设计公式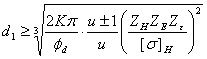：  （mm）     (8-9)

对于标准直齿轮，，  ∴分别得

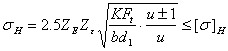    Mpa    (8-8a)

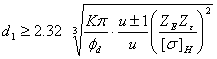     (mm)     (8-9a)

　

四、齿轮传动强度计算说明：

1、弯曲强度计算，要求， ，公式（8-5b）对大小齿轮，其它参数均相同只有不同，应将和中较大者代入计算。

2、接触强度计算公式中，，

3、轮齿面——按齿面接触疲劳强度设计，再校核齿根弯曲疲劳强度

   硬齿面——按齿根弯曲疲劳强度设计，再校核齿面接触疲劳强度

或分别按两者设计取较大者参数为设计结果（书本）

4、在用设计公式定d₁或m时，∵、、预先未知→试取载荷系数K_t代K（一般K_t=1.2~1.4）→计算得d₁(m_n)论为d_1t(m_nt)→按d_1t计算v查、、→计算，若K与K_t相差较大，则应对d_1t(m_nt)进行修正。

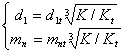  （这里考虑斜齿轮的一般情况）

5、在其它参数相同的条件下，弯曲疲劳强度与m成正比，接触疲劳强度与d₁（i一定）或中心距a成正比，即与mz乘积成正比，而与m无关

例：m=2，Z₁=40，Z₂=80；m=4，Z₁=20，Z₂=40。两对齿轮接触疲劳强度是相同的。

　

上一节

下一节